728x90
반응형
벡터란?
- 숫자를 원소로 가지는 리스트 또는 배열
$$ x = \begin{bmatrix}x_{1}\\x_{2}\\...\\x_{d}\\ \end{bmatrix} $$
$$x^{T} = \begin{bmatrix}x_{1}&x_{2}&...\\ \end{bmatrix}$$
- 공간에서의 한 점

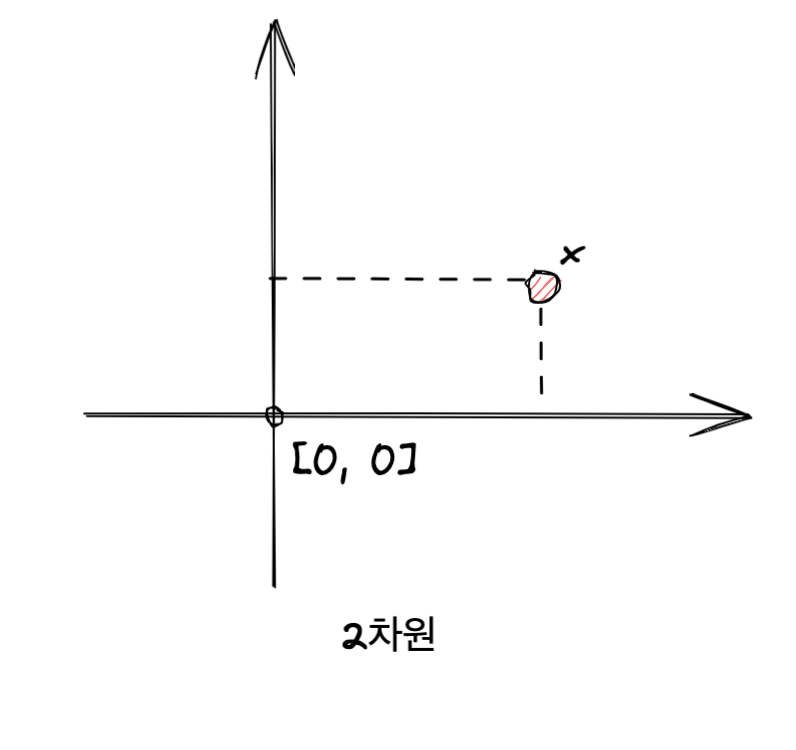
- 원점에서부터의상태적 위치
벡터 연산
- 같은 모양을 가지면 벡터 간의 덧셈, 뺄셈, 성분곱(Hadamard product) 계산 가능

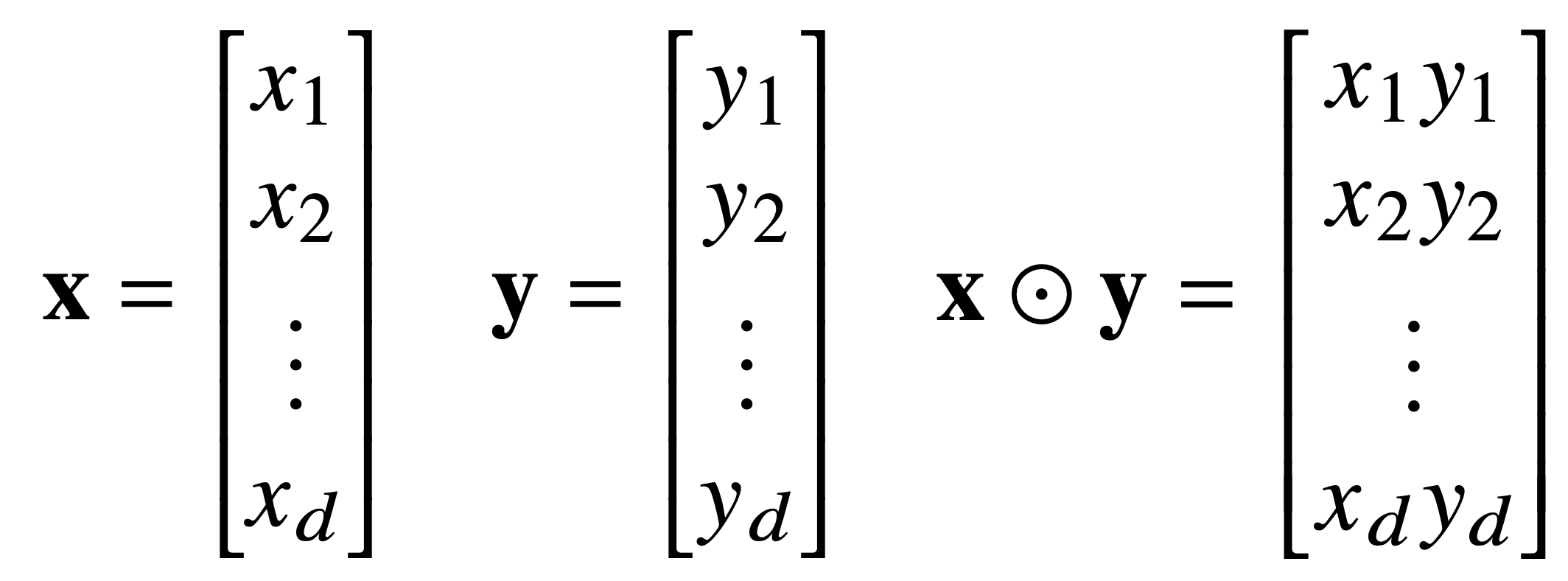
- 놈 (norm) : 원점으로부터의 거리
- 기호 : || . ||
- 임의의 차원 d에 대해 성립 -> 차원 상관없이 계산이 가능
- 종류
- L1 norm
$$||x||_{1}=\sum_{i=1}^{d}|x_{i}|$$
각 성분의 변화량의 절댓값의 합
좌표평면에서 좌표축을 따라 움직이는 거리를 뜻함 - L2 norm
$$||x||_{2}=\sqrt{\sum_{i=1}^{d}|x_{i}|^{2}}$$
피타고라스의 정리를 이용해 유클리드 거리를 계산
원점에서 직접 연결된 선
- L1 norm
- 다른 norm을 사용하는 이유
- 노름의 종류에 따라 기하학적 성질이 달라짐
- 성질이 다른 기하 세계에서 학습을 할 경우 다른 성질이 성립됨
- 다양한 방법으로 학습 또는 정규화가 가능
- 머신러닝에서 기계학습의 목적이 다른 경우 다른 종류의 norm을 사용해야 함
ex : L1 norm - Robust 학습, Lasso 회귀 / L2 norm - Laplace 근사, Ridge 회귀

def l1_norm(x):
x_norm = np.abs(x)
x_norm = np.sum(x_norm)
return x_norm
def l2_norm(x):
x_norm = x*x
x_norm = np.sum(x_norm)
x_norm = np.sqrt(x_norm)
return x_norm
벡터 사이의 거리
L2 노름과 벡터의 뺄셈을 이용해 두 벡터 사이의 거리를 계산할 수 있다.

벡터 사이의 각도
L2 노름과 제2 코사인 법칙을 이용해 두 벡터 사이의 각도를 계산할 수 있다.
$$cos\theta = \frac{||x||_{2}^{2} + ||y||_{2}^{2}-||x-y||_{2}^{2}}{2||x||_{2}||y||_{2}}$$

분자를 쉽게 계산하는 방법으로 식을 변환한 것을 내적이다.
$$cos\theta = \frac{<x, y>}{||x||_{2}||y||_{2}}$$
$$<x, y> = \sum_{i=1}^{d}{x_i y_i}$$
def angle(x,y):
v = np.inner(x, y) / (l2_norm(x) * l2_norm(y)) # np.inner:내적
theta = np.arccos(v) # 역코사인
return theta
내적의 해석
내적은 정사영(orthogonal projection)된 벡터의 길이와 관련이 있다. 또한 두 벡터의 유사도(similarity)를 측정하는 데 사용 가능한데 이는 두 데이터 또는 패턴이 얼마나 유사한가?라는 문제를 해결할 때 사용할 수 있다.

Proj(x)는 벡터 y로 투영된(정사영된) 벡터 x의 그림자를 의미한다.
Proj(x)의 길이는 코사인 법칙에 의해 $$||x||cos\theta$$가 된다

내적은 정사영의 길이를 벡터 y길이 ||y||만큼 조정한 값이다.
$$ <x, y> = ||x||_{2}||y||_{2}cos\theta $$
728x90
반응형
'Analysis' 카테고리의 다른 글
| [그래프] 1-2. 필수 기초 개념 (0) | 2022.09.27 |
|---|---|
| [그래프] 1-1. 그래프 이론기초 (0) | 2022.09.26 |
| [논문리뷰]Learning to Propagate Labels: Transductive Propagation Network for Few-shot Learning (0) | 2022.07.27 |
| [논문리뷰] FixMatch : Simplifying Semi-Supervised Learning with Consistency and Confidence (0) | 2022.07.19 |
| Skewness, 비대칭 데이터 (0) | 2022.07.17 |



