문제인식
최근 관심을 받고 있는 few-shot learning은 각 클래스별 제한된 수의 데이터만으로 분류기를 잘 일반화 하는 것이다. 관련하여 다수의 다중 클래스 데이터로 학습하고 일반화하는 meta-learnig이 많이 사용되고 있지만 여전히 최신의 분류 문제에는 데이터가 적은 문제가 남아있다.
본 연구에서 제안하는 것은 전도성 전파망(Transductive Propagation Network, TPN)을 이용해 전체 데이터를 추론에 이용하는 meta-learning을 제안한다.
배경 개념
Few-shot learning 용어 정리
- N-way K-shot
- way : Class 개수
- shot : class당 제공하는 입력 데이터의 수
- 대부분의 연구들이 5-way 1-shot / 5-way 5-shot을 벤치마크로 함

- source, support set : 학습 데이터
- query set : 밸리데이션 데이터
- 주요 학습 방법
- Transfer Learning
- Meta Learning

Meta-Learning
- 배치 데이터를 학습하는 것이 아닌 여러개의 Task를 동시에 학습하면서 각 Task 간의 차이도를 학습한다.
- 전체 학습 이후 소량의 데이터(few-shot)로도 추론할 수 있는 범용적인 모델을 생성할 수 있다.
- Meta-learning 학습 과정에서는 전체 데이터를 여러개의 support set, query set으로 쪼개는 과정이 필요한데 이를 통해 에피소드 학습(episode training)을 진행한다.
- 잘 알려진 방법은 MAML (Finn et al., 2017) : 민감한 parameter를 이용해 전이할 수 있는 대표성을 찾는 것

- 이전에 제시되었던 방법과 비교해 본 연구에서는 query point 의 라벨 전이를 위해 closed-form 방법을 사용했다. 또한 내부 업데이트 시 gradient computation을 피해 일반적으로 더 좋은 성능이 나왔다고 언급한다.
Transfer Learning
- Pre-trained 모델을 중심으로 학습하여 소량의 데이터로 각각의 task에 맞게 재학습 하여 fine tunning 하는 알고리즘

Embedding and Metric Learning Approaches
- meta-learning의 학습 방법은 크게 세가지가 있다
Model-based approad Metric-based approach Metric-based approach 핵심
아이디어memory embedding function,distance gradient descent 설명 모델 내,외부에 기억장치를 사용해서 학습 속도 조절 학습 데이터를 저차원 공간에 매핑(embedding) → 거리를 이용한 분류 각각의 task에 최적 파라미터 서치
Transduction
- transduction이란 무언가를 다른 형태로 바꾸는 것을 뜻한다.
- 지도 학습의 범주인 귀납(induction)추론은 주어진 데이터에서 함수를 유도하는데 반해 변환(transduction)은 주어진 데이터에서 관심있는 점에 대해 알려지지 않은 함수의 값을 유도하는 것이다.
- 즉 Inductive는 획득한 training case를 통해 일반적인 룰을 학습하고, test 단계에서 그 룰을 활용하여 이전에 보지못한 test case를 추론
- Transduction은 위와는 조금 차이가 있음. 일반적인 룰을 사용하여 추론하기 보다는 관찰된 특정한 training 케이스를 사용해서 관찰되지 않은 특정한 training 케이스를 추론하는 과정으로 볼 수 있음 ⇒ support set만을 이용해 학습하고 query set을 분류한다면 inductive / support, query에 의존해 query를 추론하면 transductive inference

TPN(Transductive Propagation Network)의 제안 방법
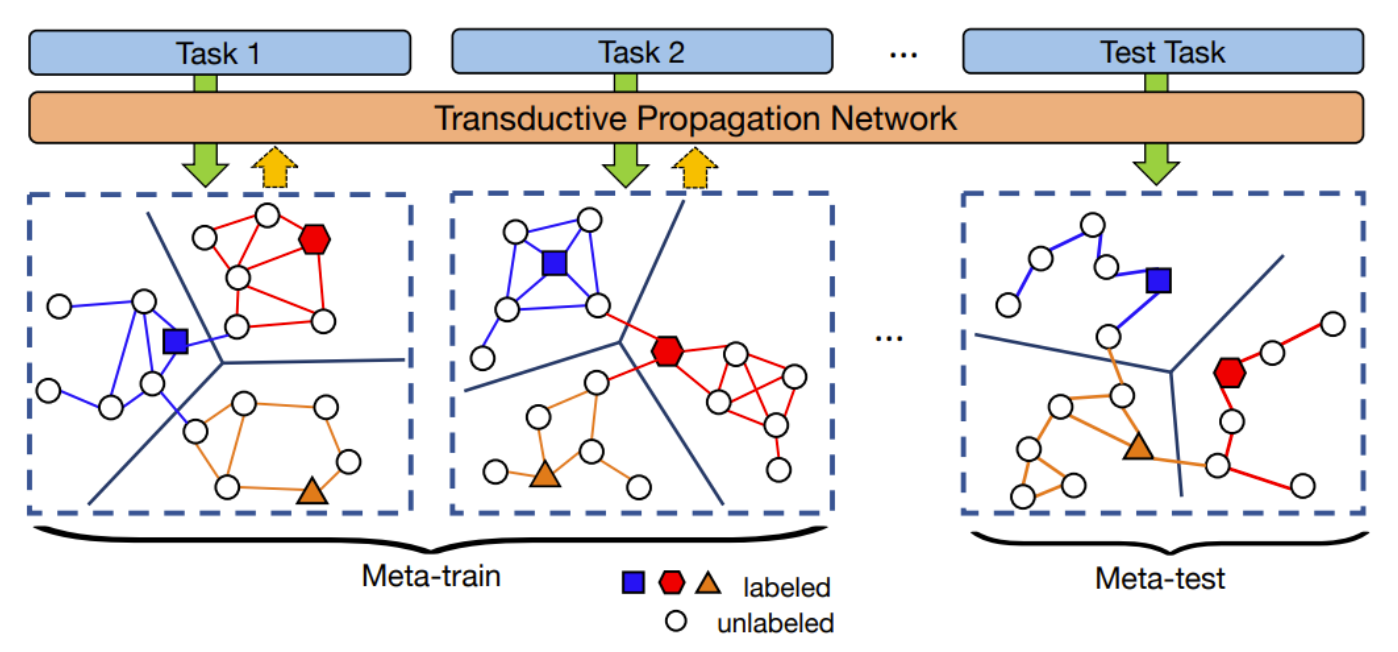
Transductive meta-learning의 컨셉
노드를 연결하는 선은 그래프 연결을 뜻하고 색은 잠재적인 label 전이 방향을 뜻한다. neighborhood 그래프는 에피소드 별로 학습된다.
전도성 전파망은 크게 4가지 파트로 나눌 수 있다.
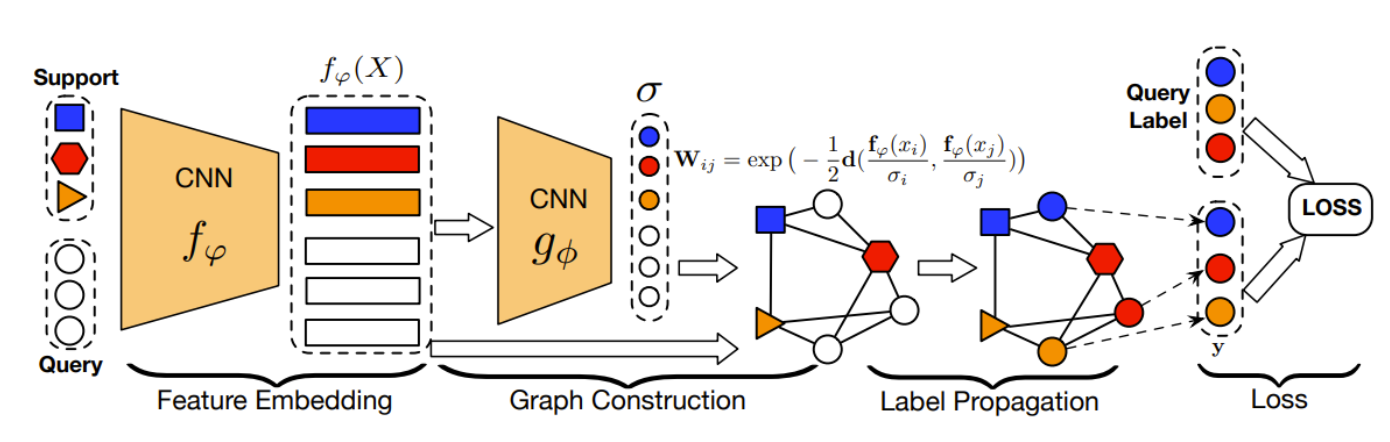
- Feature Embedding : CNN 사용한 피쳐 추출
- Graph Construction : 매니폴드 구조를 이용하기 위해 example-wise parameter를 생성하는 그래프 구조
- Label Propagation : support set에서 query set으로 label 전이
- Loss : 전이된 label과 원래 label의 cross entropy 를 계산하는 부분
Feature Embedding
- input $x_{i}$에서 feature를 추출하기 위해 CNN 사용
- 이미지의 주요한 특징을 feature vector 형태로 뽑아냄
- $f_{\phi}(x_{i}; \phi)$ : feature map ($\phi$ : 네트워크의 파라미터)
- tansductive 접근의 효과를 강조하기 위해 몇몇 연구에서 공통적으로 사용된 구조 사용
- 4개의 convolution block
- 각 block은 2D convolution layer, 3*3 kernel, filter size 64
- 각 convolution layer 다음에는 batch-normalization, ReLU, 2*2 max-pooling layer 적용
- S, Q에 동일한 embedding function $f_{\phi}$적용
Graph Construction
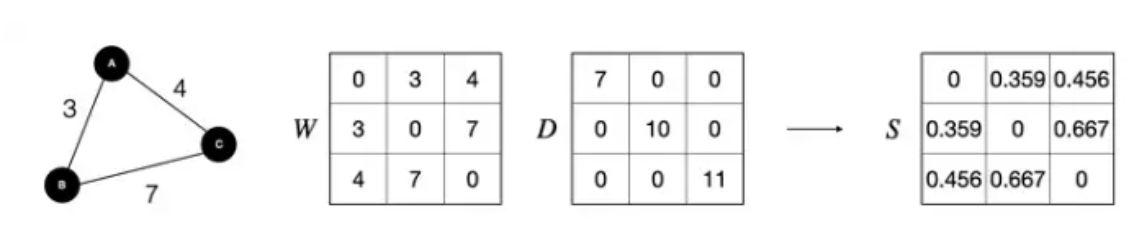
- 두 데이터간의 유사도를 구하는 과정
- example-wise length-scale parameter
- 이 때 유사도에 큰 영향을 미치는 인자는 sigma($\sigma$)라는 example-wise length-scale parameter 이다. 이 $\sigma$를 구하기 위해 이전 단계에서 구한 feature vector를 또다른 CNN의 input으로 하여 얻을 수 있다. $\sigma_{i} = g_{\phi}(f_{\phi}(x_i))$
- TPN에서는 기존 similarity matrix로 흔히 사용되는 gaussian similarity function 대신 수정하여 사용한다.
- (gaussian similarity) $W_{ij} = exp(-\frac{d(x_{i}, x_{j})}{2\sigma^2})$ ⇒ (TPN) $W_{ij} = exp(-\frac{1}{2}d(\frac{f_{\phi}(x_i)}{\sigma_i}, \frac{f_{\phi}(x_j)}{\sigma_j}))$
- 수정된 식을 보면 기본적으로 데이터간의 거리를 이용해 유사도를 보지만 노드(데이터)간 거리를 그대로 보는 것이 아닌 scailing parameter인 sigma를 통해 노드 값을 각 task에 조정한 뒤 유사도를 계산한다.
- ⇒ 이번 단계에서는 이런 feature가 들어왔으니 sigma를 이렇게 뽑아 feature를 조정해서 그래프를 구성해야 겠구나!
- 만들어진 similarity matrix는 다시 Laplacian matrix를 이용해 similarity matrix를 normalize 한다. →$S = D^{-1/2}WD^{-1/2}$, D: 대각행렬
- Graph construction in each episode

- few-shot meta-learning을 위해 에피소드 패러다임을 따름 → 각 에피소드 task별로 개별 그래프를 구축
Label Propagation
- 이전 단계에서 얻은 normalized graph laplacian S를 사용해 support set노드의 label을 query set의 unlabel 노드로 전파
- 해당 단계에서는 trainable parameter가 존재하지 않음
- 계산식
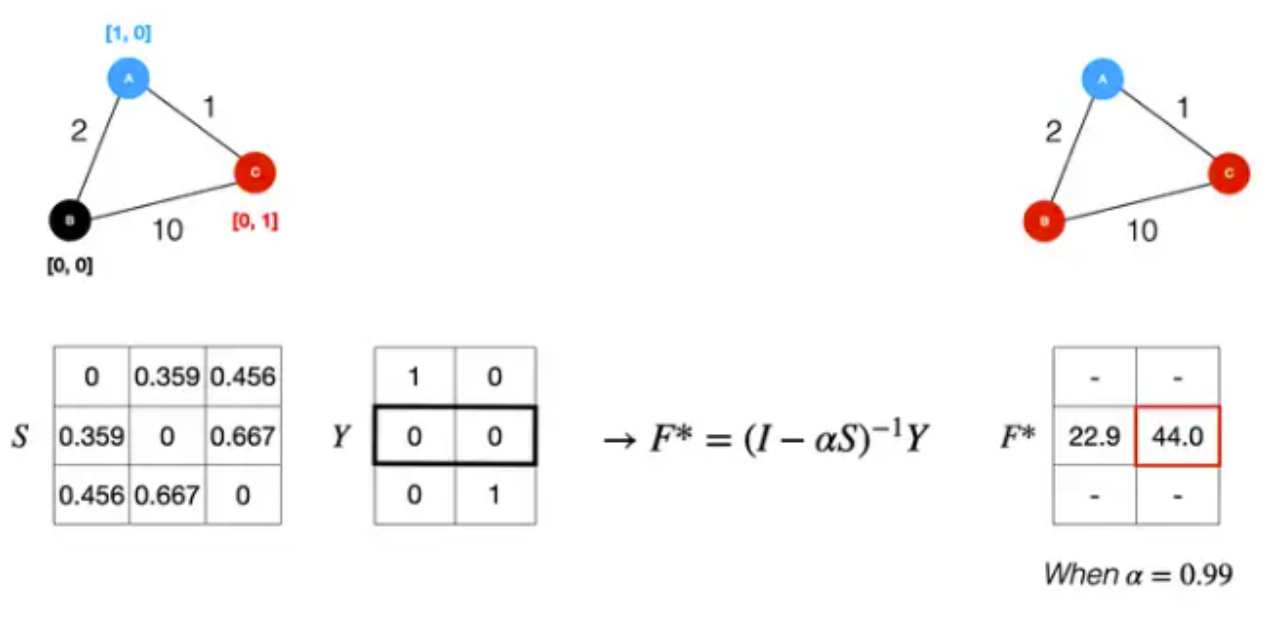
- f : 양수의 값만을 가지는 (N*K+T) * N 크기의 행렬세트
- Y는 $x_i$가 support set에 속하고, $y_i = j$인 경우 ⇒ 해당 entry값이 1인 label matrix
- F : timestep t에서 prediction matrix
- $\alpha$ : propagated information양을 조절하기 위한 hyperparameter(0~1) / 실험에서는 0.99
- $F_{t+1} = \alpha SF_t + (1-\alpha)Y$
- 충분한 timestamp을 지난 후 식의 재구성
- $F^* = (1 - \alpha S)^{-1} Y ,$ for classification
- 닫힌 형태 → iteration없이 바로 계산 가능
- 시간 복잡도 : 역행렬 계산은 $O(n^3)$의 시간 복잡도를 가지는 비효율적인 계산이지만 few-shot learning의 경우에는 n이 많은 경우에도 100정도로 작음 (1-shot:80 / 5-shot:100)
- $F^* = (1 - \alpha S)^{-1} Y ,$ for classification
Loss
- label propagation 단계에서 계산된 $F^*$를 ground-truth label 과 비교 → cross-entropy loss 계산
- loss 계산 시 query set만 사용하는 것이 아닌 support set도 함께 사용 (기존 few-shot learning은 support set으로 추론 → query set만을 사용해 loss뽑음)
결론 및 의의
- Transductive inference를 few-shot learning에 명시적으로 적용한 최초의 논문 2018년 Nichole의 논문에서 transductive 세팅 실험을 진행했지만 직접적인 transductive model이 아닌 배치 정규화를 통해 query 예제의 정보만 공유했을 뿐이다
- transductive inference 상황에서 episodic meta-learning을 통해 보이지 않는 class의 데이터 인스턴스에 label 전파 방법을 학습하는 label progapation graph를 제안했다. 이는 2004년 제안된 naive heuristic-based label propagation methods 연구의 성능을 훨씬 앞질렀다.
- few-shot 연구의 벤치마크인 miniImageNet, tieredImageNet에 대해 각각 state-of-the-art 성능을 보였고 SSL 실험에서도 높은 성능을 보였음
Experiements
데이터셋
- miniImageNet
- 클래스 100개 / 클래스당 600개 샘플
- tieredImageNet
- 클래스 600개 / 클래스당 평균 1281개
실험 세팅
- 다른 기능의 비교를 위해 feature embedding 함수로 널리 사용되는 CNN(Finn, 2017) 사용.
- $\alpha$=0.99
- 초기 learning rate = $10^{-3}$
- miniImageNet : 10,000 에피소드 마다 1/2 감소
- tieredImageNet : 25,000 에피소드 마다 1/2감소
- shot
- training : 5-shot / 10-shot
- test : 1-shot / 5-shot
Few-shot 분류 정확도 결과
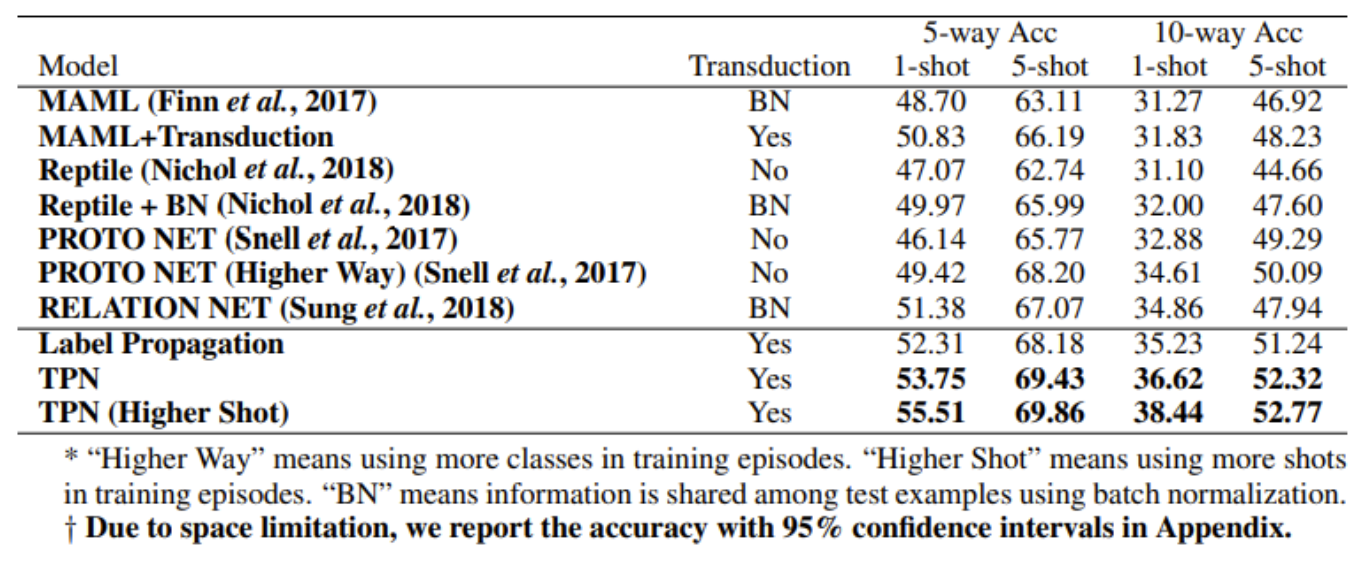
- miniImageNet
- 600개 테스트 에피소드의 평균
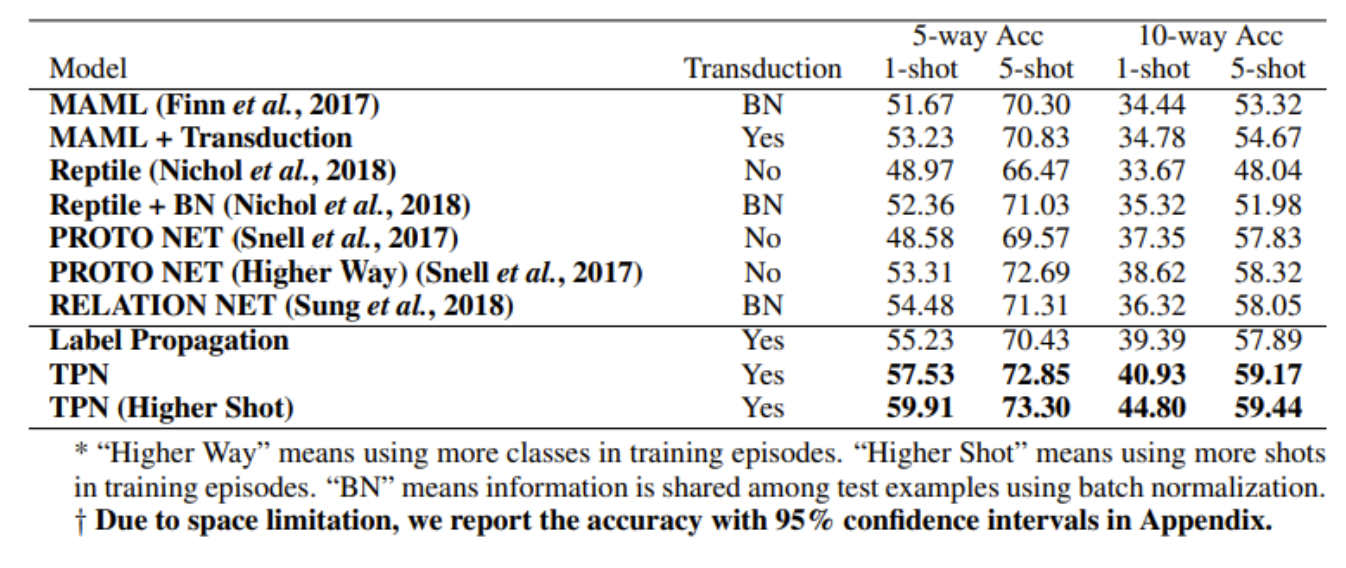
- tieredImageNet
- 600개 테스트 에피소드의 평균
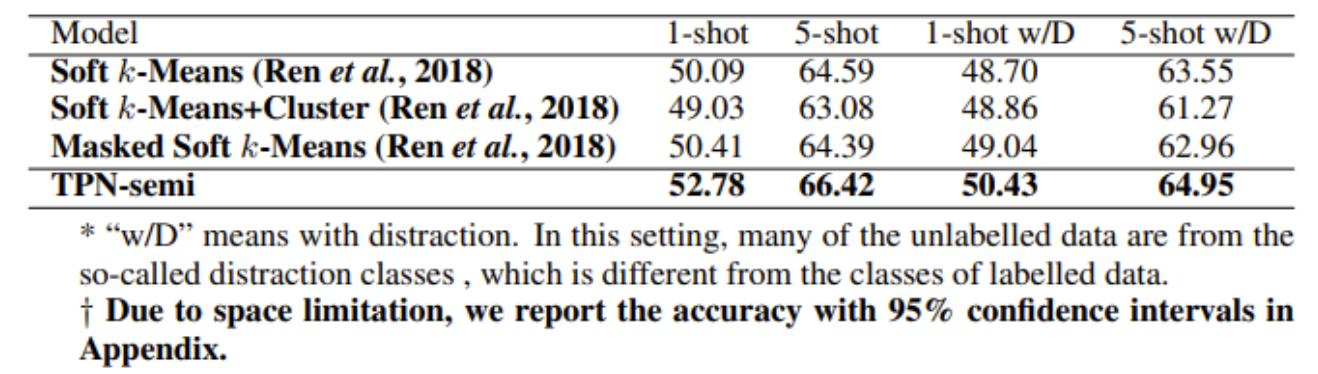
Semi-supervised few-shot 결과
- miniImageNet
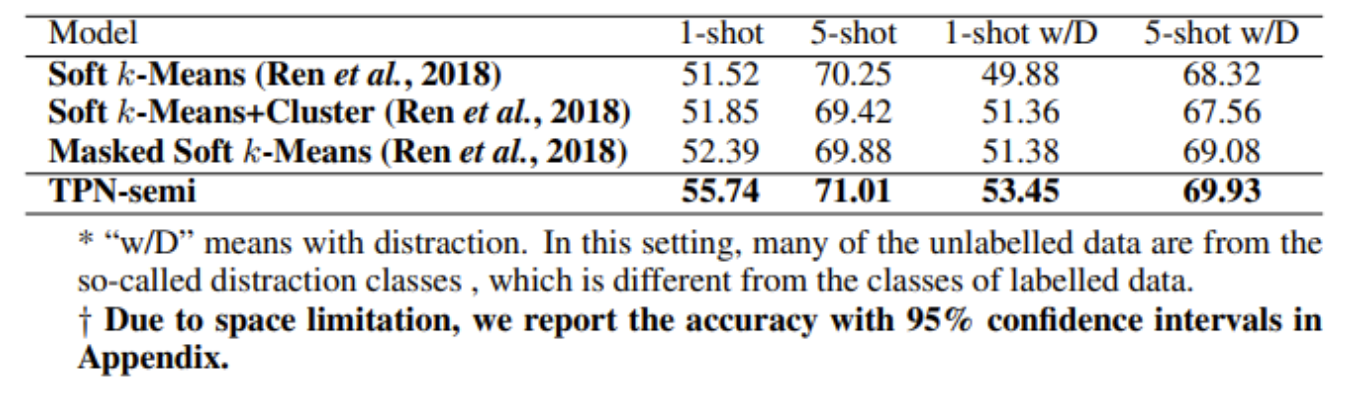
- tieredImageNet
Reference
https://yuhodots.github.io/deeplearning/21-03-04/
https://meta-learning.fastforwardlabs.com/#meta-learning%3A-learning-to-learn
'Analysis' 카테고리의 다른 글
| [그래프] 1-2. 필수 기초 개념 (0) | 2022.09.27 |
|---|---|
| [그래프] 1-1. 그래프 이론기초 (0) | 2022.09.26 |
| [논문리뷰] FixMatch : Simplifying Semi-Supervised Learning with Consistency and Confidence (0) | 2022.07.19 |
| 벡터 (0) | 2022.07.18 |
| Skewness, 비대칭 데이터 (0) | 2022.07.17 |



